Polygenic prediction via Bayesian regression and continuous shrinkage priors
·Deriving realistic Polygenic Risk Scores
With the publications of multiple large scale GWAS studies (i.e UK Biobank), new software are developed to integrate these big data sets and previous smaller scale studies. The latest breakthrough PRS-CSx enable cross-population analyses to identify disease causing SNPs in Asian populations.
The whole area is interesting, yet completely new to me, so let me get a few things straight before going into the codes.
Here is the extract from the latest review by Collister et al (2022):
1) Polygenic risk score (PRS) is a metric on an individual risk factor of developing a trait (disease) based on his/her SNP panel.
2) Gene effect ($\beta$) usually denotes an effect of a SNP (filtered from GWAS) that associated with the trait, the PRS is derived from summing up the $\beta$ over all surveyed SNP.
\[\sum_{i=1}^{N} \beta_i * dosage_ij\]3) $\beta$ is estimated from GWAS data and selected based on their p-values as causal SNPs. Here the GWAS is the base data, which is a representation of the underlying population’s genetic structures (i.e base compositions/ bottleneck effects/Linkage disequilibrium) and also where most surveyed samples do not carry the traits.
4) To tune $\beta$ s’ association with a disease, target data is usually employed with fewer samples and surveying fewer number of SNPs but has a case/control design. There is usually no overlaps between target and base data.
5) The performance of PRS is evaluated by R2 or ROC on case/control datasets.
PRS-CS
The key for PRS is to accurately inference the effect of a SNP $\beta$ towards a phenotype, which are constrained by 1) LD and 2) experimental noise. The innovation here is about shrinkage: reduce hitchhiking snps’ $\beta$ to zero. This is exactly what PRS-CS (Ge et al (2019)) is dedicated to do and look at their methods:
PRS-CS is a Bayesian regression model that uses continuous shrinkage (something looks like a numeral norm ||x||n) to tune $\beta$. The continuous shrinkage prior models the distribution of individual SNPs effect that peaks at 0, showing most snps has negligible effects, and a long tail indicating that a small number of snps has causal effects. PRS-CS combines LD information (matrix D as I is all markers are unlinked), a global shrinkage factor $\phi$ and individual tuning factor $\psi$ for each snp. $\phi$ and $\psi$ formulate the shape parameters that describe the distribution of $\beta$, which would convert to a Beta distribution with shape $\alpha$ and rate $b$, in the paper that best combination is a = 1 and b = 1/2.
After setting up the model, 1000-10000 iteration of MCMC is run with 500 burn-in were performed.
The code
So in the github, the PRS-CS has 2 parts: phrasing the input and then perform the MCMC.
We first need the the LD reference (i.e. from 1000 human genome project). PRS-CS provides that already for us.
We also have the snpinfo_1kg_hm3 (from the 1000 project) that the MAF of each SNP is documented.
Then, we need to GWAS summary stats file (where the initial BETA has been estimated).
Alternatively, BETA can be effect/odds ratio of the A1 allele.
The example sum.txt has 1000 SNPs for chr 22 and the P values are everywhere, thus no p-thresholding was done a prior.
And finally, we have the text.bim file that specified the SNPs present in the target data or inferring PRS later.
parse_genet.py
import os
import scipy as sp
from scipy.stats import norm
from scipy import linalg
import h5py
import numpy as np
### read in LD ref ###
def parse_ref(ref_file, chrom):
print('... parse reference file: %s ...' % ref_file)
ref_dict = {'CHR':[], 'SNP':[], 'BP':[], 'A1':[], 'A2':[], 'MAF':[]}
with open(ref_file) as ff:
header = next(ff)
for line in ff:
ll = (line.strip()).split()
if int(ll[0]) == chrom:
ref_dict['CHR'].append(chrom)
ref_dict['SNP'].append(ll[1])
ref_dict['BP'].append(int(ll[2]))
ref_dict['A1'].append(ll[3])
ref_dict['A2'].append(ll[4])
ref_dict['MAF'].append(float(ll[5]))
print('... %d SNPs on chromosome %d read from %s ...' % (len(ref_dict['SNP']), chrom, ref_file))
return ref_dict
ref_file="./ldblk_1kg_eur/snpinfo_1kg_hm3"
ref_dict=parse_ref(ref_file, 22)
>>> 16464 SNPs on chromosome 22 read from ./ldblk_1kg_eur/snpinfo_1kg_hm3
### read in test.bim - target dataset
def parse_bim(bim_file, chrom):
print('... parse bim file: %s ...' % (bim_file + '.bim'))
vld_dict = {'SNP':[], 'A1':[], 'A2':[]}
with open(bim_file + '.bim') as ff:
for line in ff:
ll = (line.strip()).split()
if int(ll[0]) == chrom:
vld_dict['SNP'].append(ll[1])
vld_dict['A1'].append(ll[4])
vld_dict['A2'].append(ll[5])
print('... %d SNPs on chromosome %d read from %s ...' % (len(vld_dict['SNP']), chrom, bim_file + '.bim'))
return vld_dict
bim_file="./test_data/test"
vld_dict=parse_bim(bim_file, 22)
>>>... 1000 SNPs on chromosome 22 read from ./test_data/test.bim
###phrase sumstats
n_gwas=200000 ### directly extract from example command
sst_file="./test_data/sumstats.txt"
def parse_sumstats(ref_dict, vld_dict, sst_file, n_subj):
print('... parse sumstats file: %s ...' % sst_file)
ATGC = ['A', 'T', 'G', 'C']
sst_dict = {'SNP':[], 'A1':[], 'A2':[]}
with open(sst_file) as ff:
header = next(ff)
for line in ff:
ll = (line.strip()).split()
if ll[1] in ATGC and ll[2] in ATGC:
sst_dict['SNP'].append(ll[0])
sst_dict['A1'].append(ll[1])
sst_dict['A2'].append(ll[2])
print('... %d SNPs read from %s ...' % (len(sst_dict['SNP']), sst_file))
mapping = {'A': 'T', 'T': 'A', 'C': 'G', 'G': 'C'}
vld_snp = set(zip(vld_dict['SNP'], vld_dict['A1'], vld_dict['A2']))
ref_snp = set(zip(ref_dict['SNP'], ref_dict['A1'], ref_dict['A2'])) | set(zip(ref_dict['SNP'], ref_dict['A2'], ref_dict['A1'])) | \
set(zip(ref_dict['SNP'], [mapping[aa] for aa in ref_dict['A1']], [mapping[aa] for aa in ref_dict['A2']])) | \
set(zip(ref_dict['SNP'], [mapping[aa] for aa in ref_dict['A2']], [mapping[aa] for aa in ref_dict['A1']]))
sst_snp = set(zip(sst_dict['SNP'], sst_dict['A1'], sst_dict['A2'])) | set(zip(sst_dict['SNP'], sst_dict['A2'], sst_dict['A1'])) | \
set(zip(sst_dict['SNP'], [mapping[aa] for aa in sst_dict['A1']], [mapping[aa] for aa in sst_dict['A2']])) | \
set(zip(sst_dict['SNP'], [mapping[aa] for aa in sst_dict['A2']], [mapping[aa] for aa in sst_dict['A1']]))
comm_snp = vld_snp & ref_snp & sst_snp
### ref/alt allele accordig to vld dict
print('... %d common SNPs in the reference, sumstats, and validation set ...' % len(comm_snp))
### make sure SNP present in ref and bim file, with the correct reference and alternative allele.
### normalise SNP effect (Beta) and its sd
n_sqrt = np.sqrt(n_subj)
sst_eff = {}
with open(sst_file) as ff:
header = (next(ff).strip()).split()
header = [col.upper() for col in header]
for line in ff:
ll = (line.strip()).split()
snp = ll[0]; a1 = ll[1]; a2 = ll[2]
### skip SNP entry that has non ATGC characters###
if a1 not in ATGC or a2 not in ATGC:
continue
### process snp entry that is found in base data and target data
if (snp, a1, a2) in comm_snp or (snp, mapping[a1], mapping[a2]) in comm_snp:
if 'BETA' in header:
beta = float(ll[3])
elif 'OR' in header:
beta = sp.log(float(ll[3]))
p = max(float(ll[4]), 1e-323)
### set p -value threshold? ###
beta_std = np.sign(beta)*abs(norm.ppf(p/2.0))/n_sqrt
### standardise beta , keep sign but put beta as the folded (p/2.0) probability in a normal distribution
sst_eff.update({snp: beta_std})
elif (snp, a2, a1) in comm_snp or (snp, mapping[a2], mapping[a1]) in comm_snp:
if 'BETA' in header:
beta = float(ll[3])
elif 'OR' in header:
beta = sp.log(float(ll[3]))
p = max(float(ll[4]), 1e-323)
beta_std = -1*np.sign(beta)*abs(norm.ppf(p/2.0))/n_sqrt ### standardize Beta?
sst_eff.update({snp: beta_std})
### combine info from ref_dict to sst_eff
sst_dict = {'CHR':[], 'SNP':[], 'BP':[], 'A1':[], 'A2':[], 'MAF':[], 'BETA':[], 'FLP':[]}
for (ii, snp) in enumerate(ref_dict['SNP']):
if snp in sst_eff:
sst_dict['SNP'].append(snp)
sst_dict['CHR'].append(ref_dict['CHR'][ii])
sst_dict['BP'].append(ref_dict['BP'][ii])
sst_dict['BETA'].append(sst_eff[snp])
a1 = ref_dict['A1'][ii]; a2 = ref_dict['A2'][ii]
if (snp, a1, a2) in comm_snp:
sst_dict['A1'].append(a1)
sst_dict['A2'].append(a2)
sst_dict['MAF'].append(ref_dict['MAF'][ii])
sst_dict['FLP'].append(1)
elif (snp, a2, a1) in comm_snp:
sst_dict['A1'].append(a2)
sst_dict['A2'].append(a1)
sst_dict['MAF'].append(1-ref_dict['MAF'][ii])
sst_dict['FLP'].append(-1)
elif (snp, mapping[a1], mapping[a2]) in comm_snp:
sst_dict['A1'].append(mapping[a1])
sst_dict['A2'].append(mapping[a2])
sst_dict['MAF'].append(ref_dict['MAF'][ii])
sst_dict['FLP'].append(1)
elif (snp, mapping[a2], mapping[a1]) in comm_snp:
sst_dict['A1'].append(mapping[a2])
sst_dict['A2'].append(mapping[a1])
sst_dict['MAF'].append(1-ref_dict['MAF'][ii])
sst_dict['FLP'].append(-1)
return sst_dict
sst_dict=parse_sumstats(ref_dict, vld_dict, sst_file, n_gwas)
So now we have the combined full SNP info in sst_dict. Info entry is stored in 8 list:
>>> sst_dict.keys()
dict_keys(['CHR', 'SNP', 'BP', 'A1', 'A2', 'MAF', 'BETA', 'FLP'])
Lets look at the first entry from sumstats.txt:
SNP A1 A2 BETA P
rs9605903 T C -0.011400 1.602000e-01
It is now converted to:
CHR SNP BP A1 A2 MAF BETA FLP
22 17054720 C T 0.2594 0.0031403321462579598 1
The p-value is removed, BETA is replaced with beta_std, and FLP==1 indicates it is a comm_snp.
This part is extracting the LD information from 1000 genome project. The information is compartmented into individual files according to chromosome numbers. Here is what a typical LD file looks like.
chr_name="./ldblk_1kg_eur/ldblk_1kg_chr22.hdf5"
f=h5py.File(chr_name, 'r')
>>> f.keys()
<KeysViewHDF5 ['blk_1', 'blk_10', 'blk_11', 'blk_12', 'blk_13', 'blk_14', 'blk_15', 'blk_16', 'blk_17', 'blk_18', 'blk_19', 'blk_2', 'blk_20', 'blk_21', 'blk_22', 'blk_23', 'blk_24', 'blk_3', 'blk_4', 'blk_5', 'blk_6', 'blk_7', 'blk_8', 'blk_9']>
### it has 24 LD blocks in chromosome 22
>>> f['blk_1']
<HDF5 group "/blk_1" (2 members)>
### it has 2 lists
>>> np.array(f['blk_1']['ldblk']).shape
(262, 262)
### in 'blk_1' there is the LD matrix of 262 x 262 pairwise comparisons of SNPs ###
>>> np.array(f['blk_1']['snplist'])
array([b'rs2186521', b'rs4911642', b'rs7287144', b'rs5748662',
b'rs2027653', b'rs2379965', b'rs5747620', b'rs9605903',....], dtype='|S10')
### snplist store the snp names ###
>>> sum([len(f[i]['snplist']) for i in list(f.keys())])
16464
### this number matches with the number of SNPs in snpinfo_1kg_hm3 for CHR22.
def parse_ldblk(ldblk_dir, sst_dict, chrom):
if '1kg' in os.path.basename(ldblk_dir):
chr_name = chrom
elif 'ukbb' in os.path.basename(ldblk_dir):
chr_name = chrom
hdf_chr = h5py.File(chr_name, 'r')
n_blk = len(hdf_chr)
ld_blk = [sp.array(hdf_chr['blk_'+str(blk)]['ldblk']) for blk in range(1,n_blk+1)]
snp_blk = []
for blk in range(1,n_blk+1):
snp_blk.append([bb.decode("UTF-8") for bb in list(hdf_chr['blk_'+str(blk)]['snplist'])])
blk_size = []
mm = 0
for blk in range(n_blk):
idx = [ii for (ii, snp) in enumerate(snp_blk[blk]) if snp in sst_dict['SNP']]
### map blk LD to sst_dict ###
blk_size.append(len(idx))
if idx != []:
idx_blk = range(mm,mm+len(idx))
flip = [sst_dict['FLP'][jj] for jj in idx_blk]
ld_blk[blk] = ld_blk[blk][sp.ix_(idx,idx)]*sp.outer(flip,flip)
_, s, v = linalg.svd(ld_blk[blk])
h = sp.dot(v.T, sp.dot(sp.diag(s), v))
ld_blk[blk] = (ld_blk[blk]+h)/2
mm += len(idx)
else:
ld_blk[blk] = sp.array([])
return ld_blk, blk_size
ldblk="./ldblk_1kg_eur"
chrom="./ldblk_1kg_eur/ldblk_1kg_chr22.hdf5"
ld_blk, blk_size=parse_ldblk(ldblk, sst_dict, chrom)
>>> [ld_blk[i].shape for i in range(len(ld_blk))]
[(135, 135), (176, 176), (511, 511), (178, 178), (0,), (0,), (0,), (0,), (0,), (0,), (0,), (0,), (0,), (0,), (0,), (0,), (0,), (0,), (0,), (0,), (0,), (0,), (0,), (0,)]
>>> blk_size
[135, 176, 511, 178, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
We can see that the SNPs we are using in the test data populated in the first 4 “blk”.
So now, we have the ssd_dict, the vld_dict ld_blk and the blk_size, ready for the MCMC inference.
mcmc_gtb.py
So here the recommendation of running the test data is to run PRS-CS with a range of $\phi$ and pick the best parameter. We will run with the recommended parameter: a=1, b=0.5 and phi=1e-2. According to the paper a=1 and b=0.5 specify a quasi-Cauchy prior that appears to work well across a range of simulated and real genetic architectures.
import scipy as sp
from scipy import linalg
from scipy import random
import gigrnd
#def mcmc(a, b, phi, sst_dict, n, ld_blk, blk_size, n_iter, n_burnin, thin, chrom, out_dir, beta_std, seed):
a=1
b=0.5
phi=1e-2
n=n_gwas
n_iter=5000
n_burnin=500
thin=5 # MCMC_THINNING_FACTOR (optional): Thinning factor of the Markov chain. Default is 5, use like a learning rate in updating
chrom=22
out_dir="./test_data"
seed=123
if seed != None:
random.seed(seed)
# derived stats
beta_mrg = sp.array(sst_dict['BETA'], ndmin=2).T
maf = sp.array(sst_dict['MAF'], ndmin=2).T
n_pst = (n_iter-n_burnin)/thin
p = len(sst_dict['SNP'])
n_blk = len(ld_blk)
# initialization
beta = np.zeros((p,1))
beta+=0.01
psi = np.ones((p,1))
### set all Beta to 1 and psi to 1
sigma = 1.0
if phi == None:
phi = 1.0; phi_updt = True
else:
phi_updt = False
## set phi prior = 1 ##
beta_est = sp.zeros((p,1)) ### 1000 row of 0
psi_est = sp.zeros((p,1)) ### 100 row of 0
sigma_est = 0.0
phi_est = 0.0
beta_std = 'False'
# MCMC
for itr in range(1,n_iter+1):
if itr % 100 == 0:
print('--- iter-' + str(itr) + ' ---')
mm = 0; quad = 0.0
for kk in range(n_blk):
### for each LD blk ##
if blk_size[kk] == 0:
continue
else:
idx_blk = range(mm,mm+blk_size[kk])
dinvt = ld_blk[kk]+np.diag(1.0/psi[idx_blk].T[0])
### extract pairwise LD metric for snps in a blk, generate the scaling factor 1/phi*psi?
dinvt_chol = linalg.cholesky(dinvt) ## Return the Cholesky decomposition, L * L.H, of the square matrix a, where L is lower-triangular and .H is the conjugate transpose operator
beta_tmp = linalg.solve_triangular(dinvt_chol, beta_mrg[idx_blk], trans='T') + sp.sqrt(sigma/n)*random.randn(len(idx_blk),1)
beta[idx_blk] = linalg.solve_triangular(dinvt_chol, beta_tmp, trans='N') ## slove ax(Dinvt_chol) =b (beta_tmp)
quad += sp.dot(sp.dot(beta[idx_blk].T, dinvt), beta[idx_blk])
### scaling the gene effect beta with psi?
mm += blk_size[kk]
err = max(n/2.0*(1.0-2.0*sum(beta*beta_mrg)+quad), n/2.0*sum(beta**2/psi)) ### lost functions?
sigma = 1.0/random.gamma((n+p)/2.0, 1.0/err)
delta = random.gamma(a+b, 1.0/(psi+phi))
## sigma dn delta is that gamma on gamma TPB distribution? ##
for jj in range(p):
psi[jj] = gigrnd.gigrnd(a-0.5, 2.0*delta[jj], n*beta[jj]**2/sigma)
psi[psi>1] = 1.0
if phi_updt == True:
w = random.gamma(1.0, 1.0/(phi+1.0))
phi = random.gamma(p*b+0.5, 1.0/(sum(delta)+w))
# posterior
if (itr>n_burnin) and (itr % thin == 0):
beta_est = beta_est + beta/n_pst
psi_est = psi_est + psi/n_pst
sigma_est = sigma_est + sigma/n_pst
phi_est = phi_est + phi/n_pst
# convert standardized beta to per-allele beta
if beta_std == 'False':
beta_est /= sp.sqrt(2.0*maf*(1.0-maf))
# write posterior effect sizes
if phi_updt == True:
### not here set phi==1e-2 ###
eff_file = out_dir + '_pst_eff_a%d_b%.1f_phiauto_chr%d.txt' % (a, b, chrom)
else:
eff_file = out_dir + '_pst_eff_a%d_b%.1f_phi%1.0e_chr%d.txt' % (a, b, phi, chrom)
with open(eff_file, 'w') as ff:
for snp, bp, a1, a2, beta in zip(sst_dict['SNP'], sst_dict['BP'], sst_dict['A1'], sst_dict['A2'], beta_est):
ff.write('%d\t%s\t%d\t%s\t%s\t%.6e\n' % (chrom, snp, bp, a1, a2, beta))
# print estimated phi
if phi_updt == True:
print('... Estimated global shrinkage parameter: %1.2e ...' % phi_est )
print('... Done ...')
>>> phi_est
0.0400000000000025
OK, in my first trial I encounter an Division error in this step about inferring psi from the TPB distribution:
>>>psi[jj] = gigrnd(a-0.5, 2.0*delta[jj], n*beta[jj]**2/sigma)
ZeroDivisionError: float division by zero
The problem come from beta[jj] was set to 0 in prior, that create 0 in later calculations. I tried to set the prior with beta = 0.01 instead and now it runs. But I have pushed the baseline of beta_est from 0 to 0.01, hope that is ok? Actually, the hardest part of the maths is hidden in the gigrnd.py. So if anyone need to generate such distribution, here is the code, but I really cannot understand it much.
We can see that phi_est eventually become 0.04 from 1e-2.
So here, in every iter, we update beta for each LD blk, calculate error (err) between empirical beta (beta_mrg) and the beta now, update psi (using gigrnd), update phi. We then feed psi into the next round (dinvt = ld_blk[kk]+np.diag(1.0/psi[idx_blk].T[0])) and then subsequently update beta by beta[idx_blk] = linalg.solve_triangular(dinvt_chol, beta_tmp, trans=’N’). But then, why do we output beta_est not beta? Is that because beta is not stable due to the randomness in delta and sigma?
Conclusion
Now we have the output data.
22 rs9605903 17054720 C T 1.681529e-03
22 rs5746647 17057138 G T -1.666132e-03
22 rs5747999 17075353 C A -1.278969e-03
22 rs2845380 17203103 A G 1.131701e-03
22 rs2247281 17211075 G A 1.490959e-03
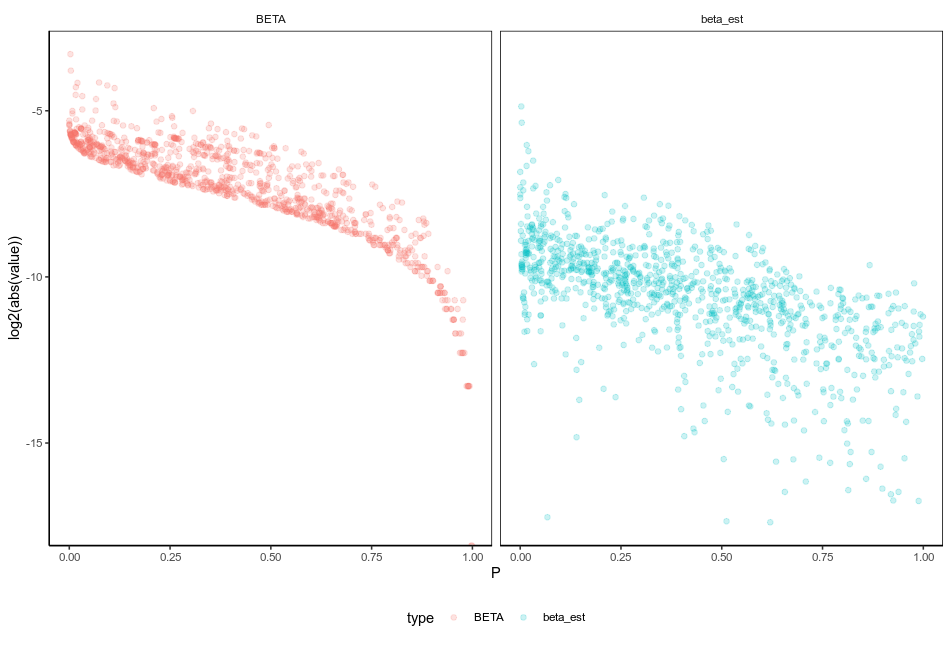
The last column is the chromosome, rs ID, base position, A1, A2 and posterior effect size estimate for each SNP. We can now use this file to calculate PRS of an individual if she or he has these SNP profiled. We can see that the corrected $\beta$ is not on average smaller by 100 fold to the original beta in sumstats.txt.
When plotted against the P values in the sumstats file, we can now see that there are more wide-spread of the $\beta$ range in beta_est, assuming that means the effect of the hitchhiking SNPs are purged, and only a few genuinely causal SNPs at the low p-value region (upper left) has most of the effect?
Going through the code, we can again see how the MCMC is conducted, and a bit of linear algebra on solving $\beta$, $\psi$ and $\phi$. We also see how the error (I bet is L2?) is calculated and how variables are updated with a learning rate. But it also show the massive gaps I have in turning these math formulas and distributions into codes, so much more to learn.