Inferring gene KO effect for many cell lines collectively

Due to work reasons, I am using MAGeCK and BAGEL in a regular basis and is introduced to this new program JACKS. The three packages infer Gene KO effects via CRISPR under 3 very different frameworks. MAGeCK computes the LFC between treatment and control sample (each treatment and controls have multiple replicates) then computes the RRA score (gene importance) via ranking the genes based on their LFC values. BAGEL requires a list of benchmark genes (essential vs non-essential) and then compute a test gene’s Bayes Factor (sum over sgRNAs for a gene) on whether the gene’s LFC is similar to the essential compared non-essential genes. The program infer then inform us whether this gene is likely to be essential or not. Then we look at the number of cell lines that the gene is deemed essential to determine the gene importance (the Adaptive Daisy Model: ADAM). These 2 packages compare 1 test sample vs 1 control sample, with multiple replicates and multiple sgRNAs per gene to ensure accuracy.

Jacks is built for a different objective. Jacks pools crisprs screens across multiple cell lines to infer 1) sgRNA efficacy x and gene effect per cell line w. Being able to separate the x sgRNA strength from the w gene effect is a nice feature. It achieve that via Bayesian variational inference on the data y (a list of LFC values per sgRNA per cell lines) based on both gene effects and sgrRNA efficacy both vary across cell lines. In that light, JACKS would helps to give us more insights into how the gene KO effect depends on the cell line’s biological properties.

running JACKs

I use the small example provided along with JACKs Github. It has 8000 sgRNAs targeting 1579 genes across 6 celllines (1 control + 5 treatments). Each gene is targeted by 1 to over 10sgRNAs, so it is quite uneven.

So let’s run it and quickly go through the results and have an understanding of what they means.

python run_JACKS.py \
example-small/example_count_data.tab \
example-small/example_repmap.tab \
example-small/example_count_data.tab \
--rep_hdr Replicate --sample_hdr Sample --common_ctrl_sample CTRL --sgrna_hdr sgRNA --gene_hdr Gene \
--outprefix small_example \
--ctrl_genes example/NEGv1.txt

The most important files are small_example_gene_JACKS_results.txt that document the gene effect (w) per cell line and their p_values listed in small_example_gene_pval_JACKS_results.txt. The p values is computed based on randomly sample the same number of negative control sgRNAs as the test genes 2000 times to establish a null distribution (using gaussian kde function) of w and compute the probability of drawing the read w.

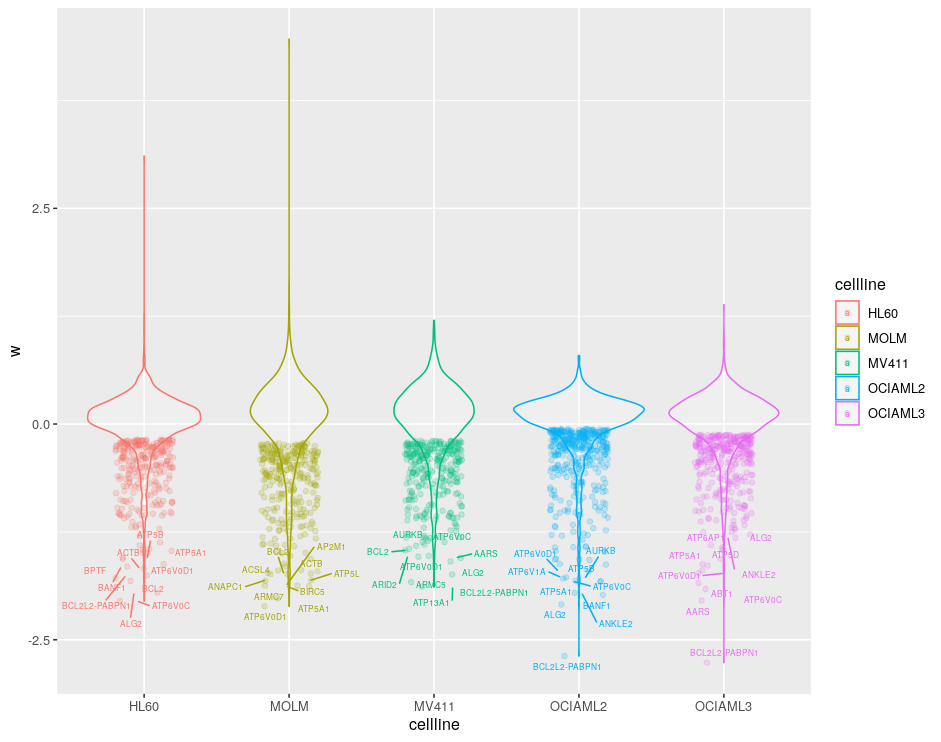
It is quite nice to see w for each cell line in a single analysis. So now lets have a look at the code on how it is done. In the small example, we could see cell line specific effects among all myeloid leukemia cell lines.

Code

The JACKs code has 3 main parts: preprocessing, infer and plot, we will focus on preprocessing and infer in this post.

preprocessing

import os, io, random, csv, argparse
import numpy as np
#def preprocess(countfile, replicatefile, guidemappingfile, rep_hdr=REP_HDR_DEFAULT, sample_hdr=SAMPLE_HDR_DEFAULT, common_ctrl_sample=COMMON_CTRL_SAMPLE_DEFAULT,#         ctrl_sample_hdr=None, sgrna_hdr=SGRNA_HDR_DEFAULT, gene_hdr=GENE_HDR_DEFAULT, ignore_blank_genes=False, outprefix=OUTPREFIX_DEFAULT, reffile=None):
# Load the specification of samples to include
countfile="example_count_data.tab"
replicatefile="example_repmap.tab"
rep_hdr="Replicate"
sample_hdr="Sample"
common_ctrl_sample="CTRL"
ctrl_sample_hdr=None
def prepareFile(filename, hdr):
    # Count any lines before the headers (should be skipped)
    f = io.open(filename)
    skip_lines, line = 0, f.readline()
    while hdr not in line and skip_lines < 100: skip_lines += 1; line = f.readline()
    f.close()
    if skip_lines >= 100:
        raise Exception('Could not find line with header ' + hdr + ' in ' + filename)
    # Check for comma vs tab delimited
    delim = ',' if (filename.split('.')[-1] == 'csv') else '\t'    
    #Reopen the file and skip to the start of the data
    f = io.open(filename); [f.readline() for i in range(skip_lines)]  
    return f, delim

f, delim = prepareFile(replicatefile, rep_hdr)
rdr = csv.DictReader(f, delimiter=delim)

sample_spec, sample_num_reps = {countfile:[]}, {}
ctrl_spec = {}
## ctrl_spec = key:treatment sample name, value=control sample name
for row in rdr:
        sample_id, rep_id = row[sample_hdr], row[rep_hdr]
        if sample_id not in sample_num_reps:
            sample_num_reps[sample_id] = 0
        sample_num_reps[sample_id] += 1
        sample_spec[countfile].append((sample_id, rep_id)) 
        if ctrl_per_sample: 
            if row[sample_hdr] in ctrl_spec:
                if ctrl_spec[row[sample_hdr]] != row[ctrl_sample_hdr]:
                    err_msg = '%s vs %s for %s\n' % (ctrl_spec[row[sample_hdr]], row[ctrl_sample_hdr], row[sample_hdr])
                    raise Exception(err_msg + 'Different controls for replicates of the sample not supported.')
            else: ctrl_spec[row[sample_hdr]] = row[ctrl_sample_hdr]
        else:
            ctrl_spec[row[sample_hdr]] = common_ctrl_sample

##
>>> ctrl_spec
{'CTRL': 'CTRL', 'MOLM': 'CTRL', 'MV411': 'CTRL', 'HL60': 'CTRL', 'OCIAML2': 'CTRL', 'OCIAML3': 'CTRL'}
>>> sample_spec
{'example_count_data.tab': [('CTRL', 'CTRL_ERS717283.plasmid'), ('CTRL', 'CTRL_AHumanV1scr_r1-altered'), ('MOLM', 'MOLM_rep_1'), ('MOLM', 'MOLM_rep_2'), ('MV411', 'MV411_rep_1'), ('MV411', 'MV411_rep_2'), ('HL60', 'HL60_rep_1'), ('HL60', 'HL60_rep_2'), ('OCIAML2', 'OCIAML2_rep_1'), ('OCIAML2', 'OCIAML2_rep_2'), ('OCIAML3', 'OCIAML3_rep_1'), ('OCIAML3', 'OCIAML3_rep_2')]}
>>> sample_num_reps
{'CTRL': 2, 'MOLM': 2, 'MV411': 2, 'HL60': 2, 'OCIAML2': 2, 'OCIAML3': 2}

So these steps are just organising the datasets.

# Load the mappings from guides to genes
#LOG.info('Loading gene mappings')
#### 
guidemappingfile="example_count_data.tab"
sgrna_hdr="sgRNA"
gene_hdr="Gene"

def createGeneSpec(guidemappingfile, sgrna_hdr, gene_hdr, ignore_blank_genes=True):
    f, delim = prepareFile(guidemappingfile, sgrna_hdr)
    rdr = csv.DictReader(f, delimiter=delim)
    gene_spec = {row[sgrna_hdr]: row[gene_hdr] for row in rdr if (not ignore_blank_genes or row[gene_hdr] != '')}
    f.close()
    return gene_spec

gene_spec = createGeneSpec(guidemappingfile, sgrna_hdr, gene_hdr, ignore_blank_genes=True)
### return dictionary Key-sgRNA, value-Gene

This block sort out the Gene:sgRNA dictionary

outprefix="example_small"
APPLY_W_HP_DEFAULT = False
NORM_TYPE_DEFAULT = 'median'
ctrl_genes=None
fdr=None
fdr_thresh_type = 'REGULAR'
n_pseudo=0
count_prior=32
positive=False

# Load negative control genes (if any)
ctrl_geneset = readControlGeneset(ctrl_genes, gene_spec) if ctrl_genes is not None else set()
ctrl_geneset =set()

# Load the data and preprocess
#LOG.info('Loading data and pre-processing')
count_prior=32
normtype='median'
###
""" Function to normalize log counts """ 
def normalizeLogCounts(logcounts, normtype='median', ctrl_guide_indexes=[]):
    G,L = logcounts.shape
    if normtype == 'median': 
        logcounts -= np.tile(np.nanmedian(logcounts,axis=0),(G,1)) # median-normalize
    return logcounts

Here, we first compute log2(count +32), then calculate the persgRNA median across replicates and then normalise the median values of each log2 count by substracting the median from it.

""" Apply a mean averaging window across a sample with a shift of 1"""
def window_smooth(m, window=25):
    ### divided the data in to 3 parts?
    ### part1 = 0 to first window, take mean
    ### part2 =  from window 2 to window(n-1): calculate var as avg of previous value (x[k-1]) and diff between 1 window (m[k+window+1]-m[k-window])
    ### part3 = last window, take mean
    ### so part1 and part3 has everyone within the window the same mean var. 
    ### part2: gradual change in variance???
    N = len(m)
    x = np.zeros(N) # mean variance in window
    for k in range(window+1): 
        x[k] = np.mean(m[0:2*window+1])
    ### 0 to window, take mean
    for k in range(window+1, N-window-1):
    ### from window 1 to window (n-1)
        x[k] = x[k-1] + (m[k+window+1]-m[k-window])/(2*window+1)
    for k in range(N-window-1, N): x[k] = np.mean(m[N-2*window-1:])
    return m


def calc_posterior_sd(data, windowfracN=100.0, do_monotonize=True, guideset_indexs=set()):
    """calculate variance of each count """
    if type(guideset_indexs) == list: guideset_indexs = set(guideset_indexs)
    MIN_WINDOW, MAX_WINDOW = 30, 800
    N = data.shape[0]
    #If there's only one replicate, set variances undefined (nans)
    if (len(data.shape) == 1 or data.shape[1] == 1):  return np.zeros(N)*np.nan
    if len(guideset_indexs) == 0: guideset_indexs = set([x for x in range(N)])
    ### guideset_indexs = number of sgRNAs ###
    window = min(max( int(len(guideset_indexs)/windowfracN), MIN_WINDOW ), MAX_WINDOW)
    ### set the number of sgRNA to be binned in the same window for variance calculation ###
    #Sort by means, then (in case of equality) variances
    means, vars = data.mean(axis=1), np.nanstd(data, axis=1)**2
    dmean_vars = [(x,y,i,(i in guideset_indexs)) for (x,y,i) in zip(means, vars, range(len(means)))]
    dmean_vars.sort()
    ### sort using asssending means ###
    dmean_vars = np.array(dmean_vars)
    # window smoothing of variances
    guideset_mask = (dmean_vars[:,3] == True)
    m =dmean_vars[guideset_mask,1]
    m = window_smooth(m, window)
    ### smooth variances in the same bin ###
    # enforce monotonicity (decreasing variance with log count) if desired
    if do_monotonize: m = monotonize(m)
    if len(guideset_indexs) != N:
        #Interpolate back up to full guide set
        m = np.interp(dmean_vars[:,0], dmean_vars[guideset_mask,0], m)
    # construct the posterior estimate and restore original ordering
    sd_post = np.zeros(N)
    sd_post[dmean_vars[:,2].astype(int)] = (m**0.5)
    return sd_post  

def condense_normalised_counts(counts, Iscreens, sample_ids):
    data = np.zeros([counts.shape[0], len(Iscreens), 2]) # mean and variance per gRNA in each sample
    ### data.shape=sgRNA x cell line x [mean, variance]
    for s, Iscreen in enumerate(Iscreens): # condense to per sample values
        N = len(Iscreen)
        data[:,s,0] = counts[:,Iscreen].mean(axis=1) # mu_hat
        data[:,s,1] = calc_posterior_sd(counts[:,Iscreen]) #sigma_hat
    return data
#Condense counts into means, variances etc per sample
sample_ids = [x for x in set(samples)]; sample_ids.sort()
Iscreens = [[col_idx for col_idx,x in enumerate(samples) if x == sample_id] for sample_id in sample_ids]
### find out which is treatment, which is control
data = condense_normalised_counts(counts, Iscreens, sample_ids)

def collateTestControlSamples(data, sample_ids, ctrl_spec):
    test_sample_idxs = [i for i,x in enumerate(sample_ids) if ctrl_spec[x] != x]
    ### isolate samples where the key and values in sample_id is different ###
    #LOG.info('Collating %d samples' % len(test_sample_idxs))
    testdata = data[:,test_sample_idxs,:]
    ctrldata = data[:,[sample_ids.index(ctrl_spec[sample_ids[idx]]) for idx in test_sample_idxs],:]    
    return testdata, ctrldata, test_sample_idxs

testdata, ctrldata, test_sample_idxs = collateTestControlSamples(data, sample_ids, ctrl_spec)   

After calculating the normalised logcounts, the code make a np.array called data that is a 8000(sgRNA) x 6 (5 treatment + control) x 2(mean, variance) dataframe. The mean value between replicates per celllines are taken and then the variances are calculated from the calc_posterior_sd() function.

It is the “moving average filter” mentioned in the paper. Here genes are arrange according to their logcounts in a cell line (low to high). Using every 800 sgRNA as a batch, it calculate the variance as the mean of variance among this 800 genes and then further normalise it by taking mean using the window_smooth() function.

Further rearrangements by the codes resulted in a testdata(8000 x 5 x 2) and a ctrldata(8000 x 5 x 2) np.arrays. The testdata contain the mean and variances of logcounts of the 5 treatment cell lines while the ctroldata is 5 repeats of the control samples of means and variances of logcounts. Now the 2 set of data are used in the variational inference in jacks_infer.py.

infer

### begining of inferJACKS
import numpy as np
import random
import scipy as SP

""" Main function from which to compute JACKS across a set of specified genes
@param gene_index {gene: [list of row indexes for the gRNAs for that gene in the testdata]}
@param testdata (num_total_grnas x num_conditions x 2) numpy array containing the mean (idx 0) and estimated variance (idx 1 ) 
         of each median normalized log-fold change
@param ctrldata Either (num_total_grnas x num_conditions x 2) numpy array containing the respective control measurements
         for each element of testdata OR a (num_total_grnas x 2) numpy array containing a common control measurement to
         be used for all conditions.
@return {gene: y, tau, x1, x2, w1, w2}, the JACKS inference results for each gene in the input gene_index""" 
fixed_x=None ### x_reference=None
n_iter=50
apply_w_hp=False
w_only=False
### begin inferJACKSGene
""" Run JACKS inference on a single gene
@param data: G x L matrix of guide effects (log2-scale difference of cell line frequency to control, assume correctly normalized); one value for each guide and line
@param yerr: G x L matrix of guide effect standard deviations
@param n_iter: number of iterations of the EM [5]
@param verbose: whether to output debug information [False]
@return length-G vector X of guide efficacies, length-L vector W of cell line effects, GxL posterior variance estimate of Y, GxL reconstruction error (Y - X x W)
"""
#def inferJACKSGene(data, data_err, ctrl, ctrl_err, n_iter, tol=0.1, mu0_x=1, var0_x=1.0, mu0_w=0.0, var0_w=1e4, tau_prior_strength=0.5, fixed_x=None, apply_w_hp = False):
    #Adjust estimated variances if needed
### Use example of a gene
gene="BFAR"
Ig = gene_index[gene]
>>> Ig
[7432, 7433, 7434, 7435, 7436]

Here, we use BFAR as an example because each gene is inferred individually for w, x, tau.

data=testdata[Ig,:,0] ### take the mean value for each sgRNA (row) x sample (col)
data_err=testdata[Ig,:,1] ### take the sd for each sgRNA (row) x sample (col)
ctrl=ctrldata[Ig,:,0] 
ctrl_err=ctrldata[Ig,:,1]
n_iter=50
tol=0.1
mu0_x=1
var0_x=1.0
mu0_w=0.0
var0_w=1e4
tau_prior_strength=0.5
fixed_x=None
apply_w_hp = False
data_err[SP.isnan(data_err)] = 2.0 # very uncertain if a single replicate

#If only 1 control replicate, use data variances for ctrls as well
ctrl_err[SP.isnan(ctrl_err)] = data_err[SP.isnan(ctrl_err)]
y = data - ctrl
### y= log2FC of treatment - ctrl 
tau_pr_den = tau_prior_strength*1.0*(data_err**2 + ctrl_err**2 + 1e-2) ### errors for sgRNA (row) x sample (col)
### probability density of tau? ###

So, first y is derived from data-ctrl as the LFC. Here we can see why the rearrangement of the ctrldata is needed here for easier np operation. tau is the variance per sgrNA per cell line so it is a 5 x 5 matrix here. w is the gene effect so it is a 1 x 5 np array (gene effect per cell line). x is the sgRNA efficacy as a 1 x 5 np array (sgRNA effect per sgRNA).

Now, we can go into the variational inference code.

#Set prior of x1 and x2. 
G,L = y.shape
if fixed_x is None:
    x1 = mu0_x*SP.ones(G) 
    x2 = x1**2


w1 = np.nanmedian(y, axis=0) ### median of the gene effect per sample, take median for each column!
tau = tau_prior_strength*1.0/tau_pr_den
w2 = w1**2

### calculate errors?
def lowerBound(x1,x2,w1,w2,y,tau):
    xw = np.outer(x1,w1)
    return np.nansum(tau*(y**2 + np.outer(x2,w2) -2*xw*y))

bound = lowerBound(x1,x2,w1,w2,y,tau)

priors of x, w, and tau are set here and the lowerbound() function here estimate the error.

""" Convenience function for matrix-vector and vector-vector dot products, ignoring Nans
@param x1 matrix or vector 1
@param x2 matrix or vector 2
@return x1 dot x2, where the summands that are NaN are ignored """ 
def nandot(x1, x2):
    if len(x1.shape) == 1 and len(x2.shape) == 2:
        x1T = SP.tile(x1, [x2.shape[1],1]).transpose()
        return SP.nansum(SP.multiply(x1T,x2), axis=0)
    elif len(x2.shape) == 1 and len(x1.shape) == 2:
        x2T = SP.tile(x2, [x1.shape[0],1])
        return SP.nansum(SP.multiply(x1,x2T), axis=1)
    elif len(x1.shape) == 1 and len(x2.shape) == 1:
        return SP.nansum(SP.multiply(x1,x2))      
    return None


def updateX(w1, w2, tau, y, mu0_x, var0_x):
    x1 = (mu0_x/var0_x + nandot((y.T).T*tau,w1))/(nandot(tau,w2) + 1.0/var0_x) ### mu0_x/var0_x == 1/1 = prior mane and var, nandot() are dot product of y * tau and w1 == empricial data; iter==50, so reuse y for 50 times?
    x2 = x1**2 + 1.0/(nandot(tau,w2)+1.0/var0_x)
    wadj = 0.5/len(x1)
    #Normalize by the median-emphasized mean of x
    x1m = x1.mean() + 2*wadj*np.nanmedian(x1) - wadj*x1.max() - wadj*x1.min()      
    #LOG.debug("After X update, <x>=%.1f, mean absolute error=%.3f"%(x1.mean(), SP.nanmean(abs(y.T-SP.outer(w1,x1))).mean()))
    return x1/x1m, x2/x1m/x1m

def updateW(x1, x2, tau, y, mu0_ws, var0_w):
    w1 = (mu0_ws/var0_w + nandot(x1,(y.T).T*tau))/(nandot(x2,tau)+1.0/var0_w)
    w2 = w1**2 + 1.0/(nandot(x2,tau)+1.0/var0_w)
    #LOG.debug("After W update, <w>=%.1f, mean absolute error=%.3f"%(w1.mean(), SP.nanmean(abs(y.T-SP.outer(w1,x1))).mean()))
    return w1, w2

def updateTau(x1, x2, w1, w2, y, tau_prior_strength, tau_pr_den):
    b_star = y**2 - 2*y*(SP.outer(x1,w1)) +SP.outer(x2,w2) 
    tau = (tau_prior_strength + 0.5)/(tau_pr_den + 0.5*b_star)   
    return tau
###

#### Variational inference###
for i in range(n_iter):
    last_bound = bound
    if fixed_x is None: x1,x2 = updateX(w1,w2,tau,y,mu0_x,var0_x) 
    if apply_w_hp and len(w1) > 1: mu0_w, var0_w = w1.mean(), w1.var()*3+1e-4  # hierarchical update on w (to encourage w's together - use with caution!)
    w1,w2 = updateW(x1,x2,tau,y,mu0_w,var0_w)
    tau = updateTau(x1, x2, w1, w2, y, tau_prior_strength, tau_pr_den)
    bound = lowerBound(x1,x2,w1,w2,y,tau)
#    LOG.debug("Iter %d/%d. lb: %.1f err: %.3f x:%.2f+-%.2f w:%.2f+-%.2f xw:%.2f"%(i+1, n_iter, bound, SP.nanmean(abs(y.T-SP.outer(w1,x1))).mean(), x1.mean(), SP.median((x2-x1**2)**0.5), w1.mean(), SP.median((w2-w1**2)**0.5), x1.mean()*w1.mean()))
    if abs(last_bound - bound) < tol:
        ### if last_bound 0 - bound < tolerance_threshold 
        break
#return y, tau, x1, x2, w1, w2

It is the trickiest part of the code where the updateX(), updateW() and updateTau are the update equations defined in the paper:

It is an invaluable step for me to finally see the codes behind these equations and see the Bayesian updates in action!

Conclusion

I think JACKS is a nice breakthrough for assigning gene effects, it use multiple biological samples to infer sgRNA effects and then provide a quantitative measures on gene effect for each sample. It would be more informative than performing BAGEL for each sample that only qualitatively infer a gene as essential and non-essential and then compare across samples.

The Bayesian inference is the key step to accuracy identify the sgRNA efficacy. That is nice and can help to design better sgRNA panel later.