Reconstruction of evolving gene variants and fitness from short sequencing reads
·Using machine learning to build haplotypes from short reads.
This time, I looked into the evoracle package (paper: Shen et al) that is a new tool for profiling genotypes in directed evolution.
The authors here address the challenge of deconstructing genotypes (combinations of mutations) evolving in a directed evolution experiment that were recorded in short read sequences as fragnmented/individual mutations with allele frequencies in different time points.
The innovation here I found is to use a transition model using pytorch to infer 1) fitness of each genotype and 2) per-timepoint frequency of each genotypes. It is actually cool to use a way to see how the authors build a model to describe the allele frequency over the course of experiment and It is time for me to try to learn how pytorch works, so lets look at the codes. From here, I would use the codes in the evoracle github examples to piece together how the allele reconstruction is done.
proposing genotypes
This is the first part of the code, phrasing the frequency table:
'''
Example use of Evoracle
'''
gene = 'cry1ac'
rl = 100
# Setup
inp_dir = 'example_data/'
out_dir = f'example_evoracle_output/{gene}_{rl}nt/'
# Load data
import pandas as pd
obs_reads_df = pd.read_csv(
inp_dir + f'{gene}_{rl}nt_obsreads.csv'
)
>>> obs_reads_df
Symbols and linkage group index 0 ... 44 46
0 .. 0 0.997783 ... 0.003460 0.012121
1 V. 0 0.002217 ... 0.003460 0.006061
2 VI 0 0.000000 ... 0.993080 0.981818
3 . 1 1.000000 ... 0.010381 0.018182
4 W 1 0.000000 ... 0.989619 0.981818
5 . 2 1.000000 ... 0.055363 0.133333
So here let’s talk about the data first. In the evoracle documentation, it is suggested that we first have sequenced a target gene subjected to directed evolution over > 10000 x coverage in each time point. Then only the mutation that has > 5% (lower bound: > 1%) at any timepoint are included in the evoracle analysis.
Finally, we have a allele frequency table, with the first column describing the alleles (ie. “..” == WT) found in a region (within a read, ie. 0) over 34 timepoints (column names: 0-46).
gts = propose_gts(obs_reads_df, proposed_gt_out_fn)
# begin propose_gts
### propose_gts parameters
params = {
'wt_symbol': '.',
'change_threshold': 0.01,
'majority_threshold': 0.5,
'split_threshold': 0.01,
'single_muts': [],
'single_mut_positions': [],
'group_to_len': {},
}
obs_marginals=obs_reads_df
setup(obs_marginals['Symbols and linkage group index'])
The setup function phrase the allele table, as follows:
### begin setup
'''
Parse Symbols and linkage group index
Consider splitting into multiple columns?
'''
def parse_nt_pos(ntp):
""" split with space is [0]==genotype, [1]==position """
[symbols, group_name] = ntp.split()
return symbols, int(group_name)
ntposs=obs_marginals['Symbols and linkage group index']
group_to_len = {}
### look like the group_to_len is dictionary that discribe the length of the genotype of a given prosition. In other words for a given position, all genotype has to have the same length by padding with WT allele
for ntp in ntposs:
symbols, group_name = parse_nt_pos(ntp)
group_to_len[group_name] = len(symbols)
### adding parameters to params
params['group_to_len'] = group_to_len
### build index for mutated positions
>>> group_to_len
{0: 2, 1: 1, 2: 1, 3: 1, 4: 1, 5: 1, 6: 3, 7: 3, 8: 2, 9: 2, 10: 1, 11: 1}
ns = sum(group_to_len.values())
### total number of positions
params['single_mut_positions'] = list(range(ns))
sorted_group_nms = sorted(group_to_len.keys())
group_to_cum_idx = {g: sum(group_to_len[gt] for gt in sorted_group_nms[:gi]) for gi, g in enumerate(sorted_group_nms)}
### cummulative mutations over positions
muts = set()
for ntp in ntposs:
symbols, group_name = parse_nt_pos(ntp)
for i, s in enumerate(symbols):
if s != '.':
# Single symbol position is sum of previous group lens and position of single symbol within current group
pos = group_to_cum_idx[group_name] + i
muts.add(f'{s} {pos}')
params['single_muts'] = sorted(list(muts))
print(f'Found {ns} unique mutation positions in {len(group_to_len)} groups ...')
###
### Found 19 unique mutation positions in 12 groups ...
###
groups = parse_read_groups(obs_marginals)
### parse_read_groups
read_groups = []
base = 0
for g, glen in sorted(group_to_len.items()):
read_groups.append(list(range(base, base + glen)))
base += glen
### here, phrase mutations and positions together
>>> read_groups
[[0, 1], [2], [3], [4], [5], [6], [7, 8, 9], [10, 11, 12], [13, 14], [15, 16], [17], [18]]
Here, we can see that all these codes are trying to organise the input mutations in the table: | | | | | | | | | | | | | | | :————–:|:—:|:–:|:–:|:–:|:–:|:–:|:—-:|:—-:|:—:|:—:|:–:|:–:| | mutation groups: | 0 | 1| 2| 3| 4| 5| 6| 7| 8| 9| 10| 11| | read_groups: | 01| 2| 3| 4| 5| 6| 789|101112| 1314| 1516| 17| 18| | mutations: | ..| .| .| .| .| .| …| …| ..| ..| .| .| | mutations: | V.| W| S| G| D| N| ..R| ..Y| .D| .S| K| L| | mutations: | VI| | | | | | .ER| I.Y| CD| KS| | | | mutations: | | | | | | | GER| IPY| | | | |
Here I am showing how the mutations are phrased in the read_groups and now we have the positional and the mutation combo info.
print(f'Proposing genotypes ...')
gts = get_default_genotypes(obs_marginals, read_groups)
### begin get_default_genotypes
#def get_default_genotypes(om_df, groups):
change_threshold = params['change_threshold']
majority_threshold = params['majority_threshold']
split_threshold = params['split_threshold']
nt_pos = obs_reads_df['Symbols and linkage group index']
gts = set()
time_cols = [col for col in obs_reads_df if col != 'Symbols and linkage group index']
###>>> time_cols
###['0', '1', '2', '3', '4', '5', '6', '7', '8', '9', '10', '11', '12', '13', '14', '15', '16', '17', '18', '19', '20', '22', '24', '26', '28', '30', '32', '34', '36', '38', '40', '42', '44', '46']
for idx in range(len(time_cols) - 1):
t0, t1 = time_cols[idx], time_cols[idx + 1]
### in 2 consecutive time point
diff = obs_reads_df[t1] - obs_reads_df[t0]
### calculate difference for each alleles
uppers = list(nt_pos[diff > change_threshold])
downers = list(nt_pos[diff < -1 * change_threshold])
up_diffs = list(diff[diff > change_threshold])
down_diffs = list(diff[diff < -1 * change_threshold])
### filter alleles using change_threshold ###
majorities = list(obs_reads_df[obs_reads_df[t1] >= majority_threshold]['Symbols and linkage group index'])
### identify major allele ###
covarying_groups = default_subgroup(uppers, up_diffs, split_threshold) + default_subgroup(downers, down_diffs, split_threshold)
### covarying_groups is a function to put genotype that change together in frequecy in a time point together: < split_threshold
for gt in covarying_groups:
gts.add(form_gt(gt, majorities, groups))
### form_gt is a function that generate possible haplottype based on covarying_groups and majorities.
single_mutants = get_all_single_mutants()
### single_mutants generate single mutation allele for each read_group
### return a set of genotype showing single mutants only
>>> get_all_single_mutants()
Adding single mutants ...
{'............Y......', '....G..............', '..................L', '.........R.........', '..............D....', '..W................', '...............K...', '..........I........', '.......G...........', '.................K.', '...S...............', '.............C.....', 'V..................', '.....D.............', '................S..', '.I.................', '...........P.......', '......N............', '........E..........'}
for sm in single_mutants:
gts.add(sm)
gts.add(params['wt_symbol'] * len(params['single_mut_positions']))
### finally add WT genotype
# end of propose_gts
>>> gts
['...................', '..................L', '.................K.', '................S..', '...............K...', '...............KS..', '..............D....', '.............C.....', '............Y......', '............YC.....', '............YCDKS..', '...........P.......', '...........PYC.KS..', '...........PYCDK...', '...........PYCDKS..', '...........PYCDKS.L', '...........PYCDKSK.', '..........I........', '..........I.YC.....', '..........IPYCDKS..', '.........R.........', '........E..........', '........E..PYCDKS..', '.......G...........', '.......G...PYCDKS..', '......N............', '......N....PYCDKS..', '.....D.............', '....G..............', '....G..........KS..', '....G......PYCDKS..', '...S...............', '...S........YC.....', '...S.......PY.D....', '..W................', '..W.......I.YCDKS..', '..W...N...I.YC.KS.L', '..W...N.ERI.YC.KSKL', '..W...NGE.I.Y..K..L', '.I.................', 'V..................', 'V............C.....', 'V...........Y......', 'V...........YC.....', 'V...........YCD....', 'V..........PYC.....', 'V..........PYC..S..', 'V..........PYC.K...', 'V..........PYCDKS..', 'V.........IPYC.K...', 'V........R..Y......', 'V.....N.ERI.YC.K..L', 'V....D....I.Y......', 'V...G......PYCD....', 'V...G......PYCDK...', 'V...G......PYCDKS..', 'V...G......PYCDKS.L', 'V...G......PYCDKSK.', 'V...G.N.E.IPYCDKS..', 'V...GD.....PYCDKS..', 'V..S........YC.....', 'V..S......I.YC.....', 'V..S.D....I.YC.K...', 'V..SG..G..I.YC.KS..', 'V.W...N.E.I.YC.K..L', 'V.W...NGE.I.YC.KS.L', 'VI.................', 'VI...........C.....', 'VI...........C.KS..', 'VI...........CD....', 'VI..........YC.....', 'VI..........YC.K...', 'VI.........PYC.....', 'VI.........PYC..S..', 'VI.........PYCDKS..', 'VI........I.YC.K...', 'VI......E....C.....', 'VI.....GE.I.YC.KS..', 'VI....N......C....L', 'VI....N...I.YC.KS.L', 'VI....N.E.I.YC.KS.L', 'VI....N.ERI.YC.KSKL', 'VI...D....IPY......', 'VI..G......PYCDKS..', 'VI.S.........C.....', 'VI.S.D....I.YC.....', 'VIW..........C.....', 'VIW.......I.YC.....', 'VIW.....E.I.YC.KS.L', 'VIW.....ERI.YC...KL', 'VIW...N...I.YC.KS..', 'VIW...N...I.YC.KS.L', 'VIW...N...I.YC.KSKL', 'VIW...N.E...YC.KS.L', 'VIW...N.E..PYCDKS.L', 'VIW...N.E.I.YC....L', 'VIW...N.E.I.YC..S.L', 'VIW...N.E.I.YC.KS..', 'VIW...N.E.I.YC.KS.L', 'VIW...N.E.I.YC.KSKL', 'VIW...N.ERI.Y..KSKL', 'VIW...N.ERI.YC.KS.L', 'VIW...N.ERI.YC.KSKL', 'VIW...NG.....C....L', 'VIW...NGE...YC.KS.L', 'VIW...NGE..PYCDKS.L', 'VIW...NGE.I.YC.KS.L', 'VIW...NGE.I.YC.KSKL', 'VIW...NGERI.YC.KS.L', 'VIW...NGERI.YC.KSKL', 'VIW..DN...I.YC.KS.L', 'VIW..DNGE.I.YC.KS.L', 'VIW.G.NGE.I.YC.KS.L', 'VIWS..N...I.YC.KS.L', 'VIWS..N.ERI.YC.KSKL', 'VIWS..NGE.I.YC.KS.L', 'VIWS.DN.E.I.YC.KS.L', 'VIWS.DN.ERI.YC.KS.L', 'VIWS.DN.ERI.YC.KSKL', 'VIWS.DNGE.I.YC.KS.L', 'VIWS.DNGE.I.YC.KSKL', 'VIWS.DNGERI.YC.KSKL']
Here, we get all the possible genotypes based on their co-varying frequency over time and also add in single mutant and WT alleles. This finished the propose_genotype function.
Now we can move into the next part of evoracle: infer_fitness_and_frequencies.
infer_fitness_and_frequencies()
import sys, string, pickle, subprocess, os, datetime, gzip, time
import numpy as np, pandas as pd
from collections import defaultdict
import torch, torchvision
import torch.nn.functional as F
from torch.utils.data import Dataset, DataLoader
from torchvision import transforms, utils
from torch.utils.tensorboard import SummaryWriter
import torchvision.utils
import torch.nn as nn
import glob
device = torch.device('cpu')
print('Device:', device)
#
log_fn = None
fold_nm = ''
#
hparams = {
'num_epochs': 1000,
'learning_rate': 0.1,
'weight_decay': 1e-5,
# learning rate scheduler
'plateau_patience': 10,
'plateau_threshold': 1e-4,
'plateau_factor': 0.1,
# If the fraction of genotypes from the previous timepoint constitutes lower than this threshold in the current timepoint, skip calculating enrichments. Too many new genotypes -- can cause instability
'dilution threshold': 0.3,
# Predicted genotype frequencies are always >0, but below this threshold are treated as 0 and ignored for calculating enrichment
'zero threshold': 1e-6,
'random_seed': 0,
'alpha_marginal': 50,
'beta_skew': 0.01,
'save_intermediate_flag': False,
'save_intermediate_interval': 50,
}
def set_random_seed():
rs = hparams['random_seed']
print(f'Using random seed: {rs}')
np.random.seed(seed = rs)
torch.manual_seed(rs)
return
def print_and_log(text):
with open(log_fn, 'a') as f:
f.write(text + '\n')
print(text)
return
Here we set all the prerequisite for pytorch. Now we can go into the part that prepare the pytorch input using function MarginalDirectedEvolutionDataset().
###def predict(obs_reads_df, proposed_gts, out_dir, options = ''):
'''
Main public-facing function.
'''
read_segments = parse_read_groups(obs_reads_df) ### == read_groups ##
#check_valid_input(obs_reads_df, read_segments, proposed_gts)
set_random_seed()
# Load data and setup
dataset = MarginalDirectedEvolutionDataset(obs_reads_df,
gts,
read_segments)
### begin MarginalDirectedEvolutionDataset
class MarginalDirectedEvolutionDataset(Dataset):
def __init__(self, df, proposed_genotypes, read_groups, training = True):
'''
Expects df with columns 'Symbols and linkage group index', and ints starting from 0 for timepoints
Batch = pair of adjacent timepoints
'''
self.read_groups = read_groups
parsed = self.parse_df(df)
self.df = df.set_index('Symbols and linkage group index')
self.orig_cols = list(self.df.columns)
self.timepoints = [int(s) for s in self.orig_cols]
self.num_timepoints = parsed['Num. timepoints']
self.num_positions = parsed['Num. positions']
self.alphabet = parsed['Alphabet']
self.len_alphabet = len(parsed['Alphabet'])
self.num_marginals = parsed['Num. marginals']
self.nt_to_idx = {s: idx for idx, s in enumerate(self.alphabet)}
self.genotypes = proposed_genotypes
self.num_genotypes = len(self.genotypes)
self.genotypes_tensor = self.init_genotypes_tensor()
# Provided to model class
self.obs_marginals = self.init_obs_marginals()
self.package = {
'nt_to_idx': self.nt_to_idx,
'num_timepoints': self.num_timepoints,
'timepoints': self.timepoints,
'genotypes_tensor': self.genotypes_tensor,
'num_genotypes': self.num_genotypes,
'len_alphabet': self.len_alphabet,
'num_positions': self.num_positions,
}
pass
#
def parse_df(self, df):
'''
Expects df with columns 'Symbols and linkage group index' (e.g., AC 2), and ints starting from 0 for timepoints.
Nucleotide can be any length, position also. They are separated by a space.
Alphabet is built from observed marginals.
'''
df=obs_reads_df
ntposs = df['Symbols and linkage group index']
rs = [col for col in df.columns if col != 'Symbols and linkage group index']
# Remove alphabet characters that are 0 in all timepoints. This requires that proposed genotypes do not contain any of these character + position combinations.
import copy
dfs = copy.copy(df)
### copy df to a new table dfs
dfs['Nucleotide'] = [s.split()[0] for s in ntposs]
## add col of the genotype to dfs ###
orig_alphabet_size = len(set(dfs['Nucleotide']))
### find out the no. of gentype for the column dfs['Nucleotide'])##
dfs['Position'] = [int(s.split()[1]) for s in ntposs]
### add a column of the genotype start position
poss = set(dfs['Position'])
### find out the no. of positions ##
dfs['Total count'] = df[rs].apply(sum, axis = 'columns')
### find the total freq of the genotype ###
dfs = dfs[['Nucleotide', 'Total count']].groupby('Nucleotide')['Total count'].agg(sum)
nts = [c for c, tot in zip(dfs.index, list(dfs)) if tot > 0]
new_alphabet_size = len(nts)
print(f'Reduced alphabet size from {orig_alphabet_size} to {new_alphabet_size}.')
print(nts)
df = df.set_index('Symbols and linkage group index')
parsed = {
'Num. timepoints': len(df.columns),
'Num. marginals': len(df),
'Alphabet': sorted(nts),
'Num. positions': len(poss),
}
return parsed
#
def init_obs_marginals(self):
'''
Init obs_marginals: (n_t, n_pos, len_alphabet)
'''
df = self.df
marginals_tensor = torch.zeros(self.num_timepoints, self.num_positions, self.len_alphabet)
### here len(rs)=34, len(poss)=12, len(nts)=28: shape= 34, 336
for t_idx, t in enumerate(dataset.orig_cols):
for pos in range(self.num_positions):
rows = [f'{nt} {pos}' for nt in self.alphabet]
### generate row names with genotype + position ##
### call row in obs_reads_df that has the same genotype i.e. all the row with "."
marginals_tensor[t_idx][pos] = torch.Tensor(df[t].loc[rows])
### df[t].loc[rows] generate a column of all the row names at time_point t, if the genotype is absent, nan returns ###
marginals_tensor = marginals_tensor.reshape(self.num_timepoints, self.num_positions * self.len_alphabet)
marginals_tensor /= self.num_positions
return marginals_tensor
# generate a tensor first with 34 time_points x position x all the alphabet (genotype)
# then reshape the tensor to time_point x flattened(position x alphabet)
def init_genotypes_tensor(self):
'''
* genotypes = (n_gt, n_pos, len_alphabet), binary
Only keep proposed genotypes that are consistent with alphabet from observed marginals.
'''
retained_gts = []
for gt_idx, gt in enumerate(self.genotypes):
###genotypes==gts
inconsistent_gt = False
for pos in range(self.num_positions):
read_group = self.read_groups[pos]
start_pos = read_group[0]
end_pos = read_group[-1]
kmer = gt[start_pos : end_pos + 1]
### extract genotype at the read_group region ###
### so there are alleles that generated from propose_default_genotype that have the wrong combinations, and thus do not correspond to obs_reads_df ###
if kmer not in self.nt_to_idx:
inconsistent_gt = True
break
if not inconsistent_gt:
retained_gts.append(gt)
#
print(f'Reduced {self.num_genotypes} genotypes to {len(retained_gts)} consistent with alphabet.')
self.genotypes = retained_gts
self.num_genotypes = len(retained_gts)
#
genotypes_tensor = torch.zeros(self.num_genotypes, self.num_positions, self.len_alphabet)
for gt_idx, gt in enumerate(self.genotypes):
for pos in range(self.num_positions):
read_group = self.read_groups[pos]
start_pos = read_group[0]
end_pos = read_group[-1]
kmer = gt[start_pos : end_pos + 1]
nt_idx = self.nt_to_idx[kmer]
genotypes_tensor[gt_idx][pos][nt_idx] = 1
genotypes_tensor = genotypes_tensor.reshape(self.num_genotypes, self.num_positions * self.len_alphabet)
return genotypes_tensor
### return a binary matrix of each allele ###
The MarginalDirectedEvolutionDataset() function generate some important objects for the later pytorch modelling:
1) self.alphabet: A list of all possible mutation symbols from all the position: [’.’, ‘..’, ‘…’, ‘..R’, ‘..Y’, ‘.D’, ‘.E.’, ‘.ER’, ‘.PY’, ‘.S’, ‘C.’, ‘CD’, ‘D’, ‘G’, ‘G..’, ‘GE.’, ‘GER’, ‘I.Y’, ‘IPY’, ‘K’, ‘K.’, ‘KS’, ‘L’, ‘N’, ‘S’, ‘V.’, ‘VI’, ‘W’]; here 28 alphabets.
2) self.num_timepoints: indexed timepoint; here range(0, 34)
3) self.obs_marginals: 34 x 336 matrix that document per timepoint frequency accross the 12 mutation groups, given the 28 possible mutations.
4) self.genotypes_tensor: 119 x 336 binary matrix describing the genotype composition across 12 groups over 28 possible mutations. Here we initially got 122 genotypes from proposed genotype, we end up with 119 after a filtering step to make sure the genotype “fit” into the 28 possible mutations. Comparing the before and after these 3 single mutants [‘………..P…….’, ‘……….I……..’, ‘.I……………..’] were filtered out because these mutant do not exist in the obs_reads_df. For example, ‘.I……………..’ referred to the position 0 that only has “..”, “V.”, and “VI” genotype, thus it is removed.
5) package: a dictionary that store everything for the pytroch model
Build and train pytorch model
model = MarginalFitnessModel(
dataset.package
).to(device)
### begin MarginalFitnessModel
class MarginalFitnessModel(nn.Module):
def __init__(self, package):
super().__init__()
self.fitness = torch.nn.Parameter(
torch.ones(package['num_genotypes']) * -1 + torch.randn(package['num_genotypes']) * 0.01
).to(device)
### random number for freqeuncy? of each genotypes ###
self.fq_mat = torch.nn.Parameter(
torch.randn(
len(package['timepoints']), package['num_genotypes']
)
).to(device)
### random frequency matrix of shape 34 x 119
self.num_genotypes = package['num_genotypes']
self.timepoints = package['timepoints']
self.num_timepoints = len(package['timepoints'])
self.len_alphabet = package['len_alphabet']
self.genotypes_tensor = package['genotypes_tensor'].to(device)
self.nt_to_idx = package['nt_to_idx']
self.num_positions = package['num_positions']
def forward(self):
'''
Forward pass.
Output
* log_pred_marginals: (n_t, n_pos, len_alphabet)
* fitness_loss: (1)
Intermediates
* log_pred_p1s: (n_t - 1, n_gt)
* d_nonzero_idxs: (n_t - 1, n_gt)
* genotypes_tensor: (n_gt, n_pos * len_alphabet), binary
Multiply with fq_mat (n_t, n_gt)
-> curr_genotype_fqs = (n_t, n_gt, n_pos * len_alphabet), float
Sum across n_gt.
-> pred_marginals: (n_t, n_pos, len_alphabet)
'''
'''
Marginals
genotypes_tensor: (n_gt, n_pos * len_alphabet), binary
Multiply with fq_mat (n_t, n_gt)
-> pred_marginals: (n_t, n_pos * len_alphabet)
'''
fqm = F.softmax(fq_mat, dim = 1)
### rescale the fq_mat (34 x 119) matrix for its column all add to one finally.
pred_marginals = torch.matmul(fqm, dataset.genotypes_tensor)
### create matrix product of fq_mat (prob of genotype per timepoint) x genotype tensor
### shape= 34 * 334
pred_marginals /= dataset.num_positions
### to make sure geontype symbol occupying the same position sum <=1 ? ###
# Ensure nothing is zero
pred_marginals = pred_marginals + 1e-10
log_pred_marginals = pred_marginals.log()
#
# Fitness
fitness_loss = torch.autograd.Variable(torch.zeros(1).to(device), requires_grad = True)
for t in range(dataset.num_timepoints - 1):
p0 = fqm[t]
p1 = fqm[t + 1]
time_step = dataset.timepoints[t + 1] - dataset.timepoints[t]
nonzero_idxs = torch.BoolTensor(
[bool(p0[idx] >= hparams['zero threshold']) for idx in range(dataset.num_genotypes)]
)
#remove alleles with too low frequency at p0 ###
p0 = p0[nonzero_idxs]
p1 = p1[nonzero_idxs]
# Ignore case where too many new genotypes by normalizing to 1. Deweight loss by 1 / sum
np1 = p1 / p1.sum()
weight = p1.sum()
if p1.sum() < hparams['dilution threshold']:
# Too many new genotypes, can cause instability in model
continue
present_fitness = torch.exp(fitness[nonzero_idxs])
input_ps = p0
# Perform 1 or more natural selection updates
for ts_idx in range(time_step):
mean_pop_fitness = torch.dot(input_ps, present_fitness)
### current allele frequency (119) . fitness (119)
delta_p = torch.div(present_fitness, mean_pop_fitness)
### a correction step? that divide present_fitness by the mean_pop_fitness?
pred_p1 = torch.mul(input_ps, delta_p)
### predict p1 frequency by p0 * corrected fitness
input_ps = pred_p1
log_pred_p1 = torch.log(pred_p1)
n_gt = np1.shape[0]
log_pred_p1 = log_pred_p1.reshape(1, n_gt)
np1 = np1.reshape(1, n_gt)
### final row from fqm ###
loss = weight * F.kl_div(log_pred_p1, np1, reduction = 'batchmean')
### loss function: KL divergence using batchmean
if loss > 1e5:
print('WARNING: Fitness KL divergence may have exploded')
fitness_loss = fitness_loss + loss
### So run from start to end of time point, tract every timepoint frequency with the next by predicted fitness values
### in every time step use pred_1 to estimate fitness_loss
fitness_loss = fitness_loss / (dataset.num_timepoints - 1)
# average cummulative loss per time step
#
# Frequency sparsity loss
fq_sparsity_loss = torch.autograd.Variable(torch.zeros(1).to(device), requires_grad = True)
# Skew by time
for t in range(self.num_timepoints):
d = fqm[t]
m = d.mean()
s = d.std()
unnorm_skew = torch.pow(d - m, 3).mean()
# minimize loss to maximize positive skew
fq_sparsity_loss = fq_sparsity_loss - unnorm_skew
fq_sparsity_loss = fq_sparsity_loss / self.num_timepoints
return log_pred_marginals, fitness_loss, fq_sparsity_loss
The model first introduces fitness: 1 x 119 vector and fqm: 34 x 119 matrix, and pred_marginals: a matrix derived from fitness * fqm = final frequency of each genotype in the end of directed evolution.
In each modeling epoch, the model takes in the updates to make a new fqm and new fitness. This generate a new pred_marginals. Given the new fqm and new fitness, the model evaluate the fitness_loss and also the sparsity loss in each timestep.
Training model and infer fitness and frequency
def train_model(model, optimizer, schedulers, dataset):
since = time.time()
model.train()
marginal_loss_f = nn.KLDivLoss(reduction = 'batchmean')
fitness_loss_f = nn.KLDivLoss(reduction = 'batchmean')
obs_marginals = dataset.obs_marginals.to(device)
num_epochs = hparams['num_epochs']
epoch_loss = 0.0
losses = []
for epoch in range(num_epochs):
print_and_log('-' * 10)
print_and_log('Iter %s/%s at %s' % (epoch, num_epochs - 1, datetime.datetime.now()))
#
running_loss = 0.0
with torch.set_grad_enabled(True):
# One batch per epoch
batch_loss = torch.autograd.Variable(torch.zeros(1).to(device), requires_grad = True)
# Predict
log_pred_marginals, fitness_loss, fq_sparsity_loss = model()
'''
Loss
1. Soft constrain matrix of frequencies to match observed marginals (performed here)
2. Loss when explaining/summarizing matrix by fitness values (performed inside model forward pass)
'''
marginal_loss = torch.autograd.Variable(torch.zeros(1).to(device), requires_grad = True)
loss = marginal_loss_f(log_pred_marginals, obs_marginals)
marginal_loss = marginal_loss + loss
if marginal_loss > 100:
print('WARNING: Marginal KL divergence might be infinite')
import code; code.interact(local=dict(globals(), **locals()))
'''
Combine loss and backpropagate
'''
batch_loss = fitness_loss + hparams['alpha_marginal'] * marginal_loss + hparams['beta_skew'] * fq_sparsity_loss
running_loss = batch_loss
batch_loss.backward()
optimizer.step()
optimizer.zero_grad()
del batch_loss
# Each epoch
marginal_loss = float(marginal_loss.detach().numpy())
fitness_loss = float(fitness_loss.detach().numpy())
fq_sparsity_loss = float(fq_sparsity_loss.detach().numpy())
epoch_loss = float(running_loss.detach().numpy())
losses.append(epoch_loss)
schedulers['plateau'].step(epoch_loss)
print_and_log(f'Loss | Marginal {marginal_loss:.3E}, Fitness {fitness_loss:.3E}, Cat. skew {fq_sparsity_loss:.3E}; Total {epoch_loss:.3E}')
# Callback
if epoch % hparams['save_intermediate_interval'] == 0:
if hparams['save_intermediate_flag']:
torch.save(model.state_dict(), model_dir + f'model_epoch_{epoch}_statedict.pt')
pm_df = form_marginal_df(log_pred_marginals, dataset)
pm_df.to_csv(model_dir + f'marginals_{epoch}.csv')
fitness = list(model.parameters())[0].detach().exp().numpy()
fitness_df = pd.DataFrame({
'Genotype': dataset.genotypes,
'Inferred fitness': fitness,
})
fitness_df.to_csv(model_dir + f'fitness_{epoch}.csv')
gt_df = form_predicted_genotype_mat(model, dataset)
gt_df.to_csv(model_dir + f'genotype_matrix_{epoch}.csv')
# Detect convergence
if epoch > 15:
if losses[-15] == losses[-1]:
print_and_log('Detected convergence -- stopping')
break
time_elapsed = time.time() - since
print_and_log('Training Completed in {:.0f}m {:.0f}s'.format(
time_elapsed // 60, time_elapsed % 60))
fitness = list(model.parameters())[0].detach().exp().numpy()
fq_mat = list(model.parameters())[1].detach().softmax(dim = 1).numpy()
pred_marginals = log_pred_marginals.exp().detach().numpy()
return fitness, fq_mat, pred_marginals
### update fqm to dataset ###
def form_predicted_genotype_mat(model, dataset):
fqm = F.softmax(model.fq_mat, dim = 1).detach().numpy()
return pd.DataFrame(fqm.T, index = dataset.genotypes)
### save pred_marginal to out_dir
def form_marginal_df(log_pred_marginals, dataset):
pred_marginals = log_pred_marginals.exp().reshape(dataset.num_timepoints, dataset.num_positions * dataset.len_alphabet).detach().numpy()
pm_df = pd.DataFrame(pred_marginals.T)
nt_poss = []
for pos in range(dataset.num_positions):
for c in dataset.alphabet:
nt_poss.append(f'{c}{pos}')
ntp_col = 'Symbols and linkage group index'
pm_df[ntp_col] = nt_poss
pm_df = pm_df.sort_values(by = ntp_col).reset_index(drop = True)
return pm_df
This is a brand-new for me to see that the model and the training part of written in separate def. I think that is also the strength of pytorch to compartmentalize the model from the training parameters.
In each epoch, the model output the log_pred_marginals, fitness_loss and fq_sparsity_loss. Then the marginal_loss of each epoch is calculated by the KL-divergence of the pred and the obs_marginal genotype frequencies.
And here there is the command batch_loss.backward() that perform the back propagation. This is hard to wrap my head on the forward and backward steps on pytorch, guess I really should go back to the tutorials to understand it.
Finally this is the inference code.
optimizer = torch.optim.Adam(
model.parameters(),
lr = hparams['learning_rate'],
weight_decay = hparams['weight_decay'],
)
schedulers = {
'plateau': torch.optim.lr_scheduler.ReduceLROnPlateau(
optimizer,
patience = hparams['plateau_patience'],
threshold = hparams['plateau_threshold'],
factor = hparams['plateau_factor'],
verbose = True,
threshold_mode = 'rel',
)
}
### generate out_dir
global model_dir
model_dir = out_dir
if out_dir[-1] != '/':
out_dir += '/'
util.ensure_dir_exists(out_dir)
global log_fn
log_fn = out_dir + '_log.out'
with open(log_fn, 'w') as f:
pass
print_and_log('model dir: ' + model_dir)
#
# Inference
print(f'Running inference ...')
fitness, fq_mat, pred_marginals = train_model(model, optimizer, schedulers, dataset)
#
#update package
package = {
'fitness': fitness,
'fq_mat': fq_mat,
'pred_marginals': pred_marginals,
'updated_proposed_gts': updated_proposed_genotypes,
'num_updated_proposed_gts': len(updated_proposed_genotypes),
'fitness_df': pd.DataFrame({
'Genotype': list(updated_proposed_genotypes),
'Inferred fitness': fitness,
}),
'genotype_matrix': pd.DataFrame(
fq_mat.T,
index = updated_proposed_genotypes,
columns = dataset.timepoints,
),
}
# Save results
for fn, df in {
'_final_fitness.csv': package['fitness_df'],
'_final_genotype_matrix.csv': package['genotype_matrix'],
}.items():
print(f'Saving {out_dir}{fn} ...')
df.to_csv(out_dir + fn)
out_fn = out_dir + f'_final_package.pkl'
print(f'Saving {out_fn} ...')
with open(out_fn, 'wb') as f:
pickle.dump(package, f)
print('Done.')
return package
So this bit of codes link everything together, I think. That it set up an Adam optimizer that will adopt the training regime. Once the optimizer is called, it trains the model (forward part) and get the back propagation using all the losses calculated in the train_model() according to the schedulers parameters.
Wow, it is quite complicated for sure. But I am glad that I have watch through it.
Output and conclusion
So we now have the final pred_fitness and pred_genotype_freq in the final output for each 119 proposed genotypes. It is quite astonishing that the observeed and predicted genotype frequency is so consistent.
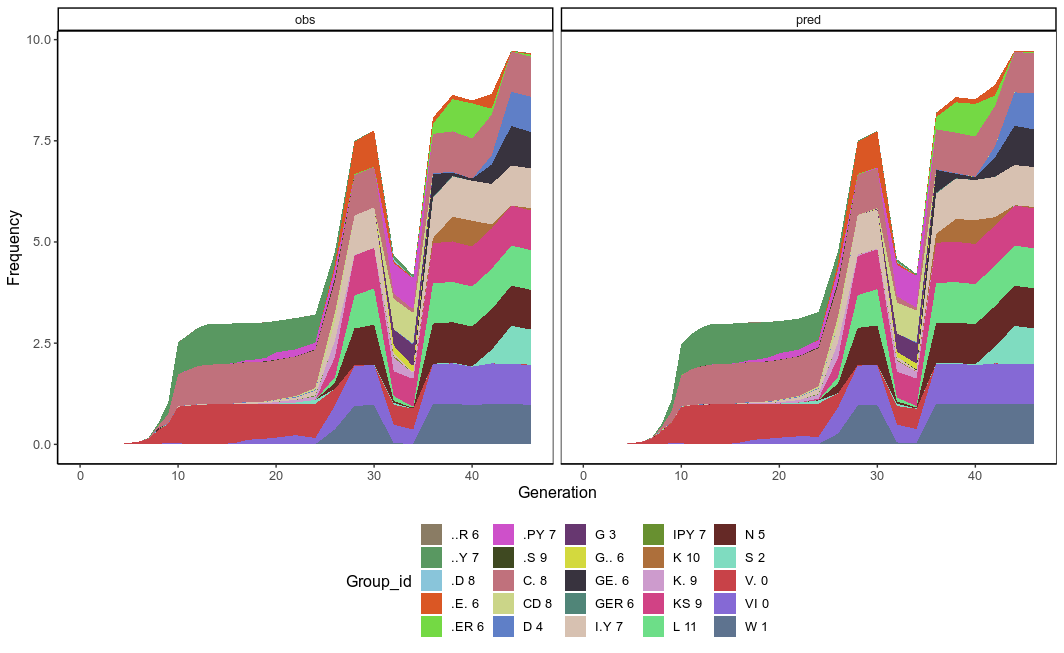
And the fittest genotype is inferred as “VIWS.DNGE.I.YC.KS.L”. the endpoint genotype that rise to the highest frequency, same as Figure1D in the paper!
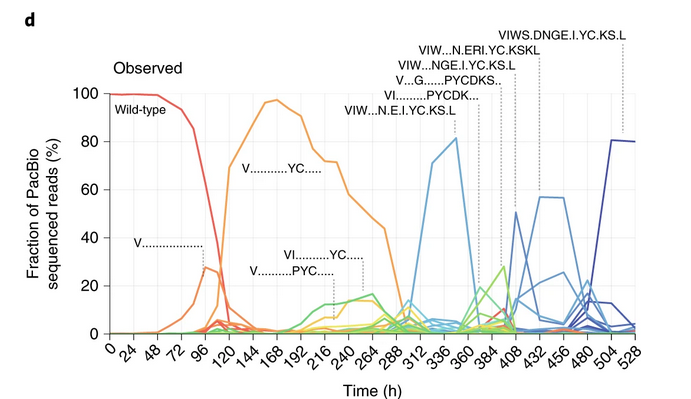
Overall, I think it is a very cool use of the ML model to reconstruct haplotype that would be otherwise hard to profile.
The pytorch code gave me some better ideas on how models are built and loss calculated, it also demonstrates a more compartmentalization of ML models and its implementation. It is quite a starting point for me to actually see how pytorch codes look like. I am very glad that I have come across this paper, and I have learnt a lot of new stuff!.